深度学习笔记（十）：SGD、Momentum、RMSprop、Adam优化算法解析

显然，参数应该是朝着目标损失函数下降最快的方向更新，更确切的说，要朝着梯度方向更新！ 假设网络参数是 $θ$ ，学习率是 $\eta$ ，网络表示的函数是 $J (θ)$ ，函数此时对 $θ$ 的梯度为： $\bigtriangledown_{ heta }J( heta)$ ，于是参数 $θ$ 的更新公式可表示为：

在这里插入图片描述

在深度学习中，有三种最基本的梯度下降算法：SGD、BGD、MBGD，他们各有优劣。

在这里插入图片描述

（1）随机梯度下降法 SGD

随机梯度下降法 (Stochastic Gradient Descent，SGD)，每次迭代（更新参数）只使用单个训练样本 $x^{(i)}, y^{(i)}）$ ，其中x是输入数据，y是标签。因此，参数更新表达式如下：

在这里插入图片描述
优点： SGD 一次迭代只需对一个样本进行计算，因此运行速度很快，还可用于在线学习。

缺点：（1）由于单个样本的随机性，实际过程中，目标损失函数值会剧烈波动，一方面，SGD 的波动使它能够跳到新的可能更好的局部最小值。另一方面，使得训练永远不会收敛，而是会一直在最小值附近波动。（2）一次迭代只计算一张图片，没有发挥GPU并行运算的优势，使得整体计算的效率不高。

（2）批量梯度下降法 BGD

批量梯度下降法 (Batch Gradient Descent，BGD)，每次迭代更新中使用所有的训练样本，参数更新表达式如下：

在这里插入图片描述
优缺点分析：BGD能保证收敛到凸误差表面的全局最小值和非凸表面的局部最小值。但每迭代一次，需要用到训练集中的所有数据，如果数据量很大，那么迭代速度就会非常慢。

（3）小批量梯度下降法 MBGD

小批量梯度下降法 (Mini-Batch Gradient Descent，MBGD)，折中了 BGD 和 SGD 的方法，每次迭代使用 batch_size 个训练样本进行计算，参数更新表达式如下：

在这里插入图片描述
优缺点分析：因为每次迭代使用多个样本，所以 MBGD 比 SGD 收敛更稳定，也能避免 BGD 在数据集过大时迭代速度慢的问题。因此，MBGD是深度学习网络训练中经常使用的梯度下降方法。

深度学习中，一般的mini-batch大小为64~256，考虑到电脑存储设置和使用的方式，如果mini-batch是2的次方，代码会运行地更快一些。
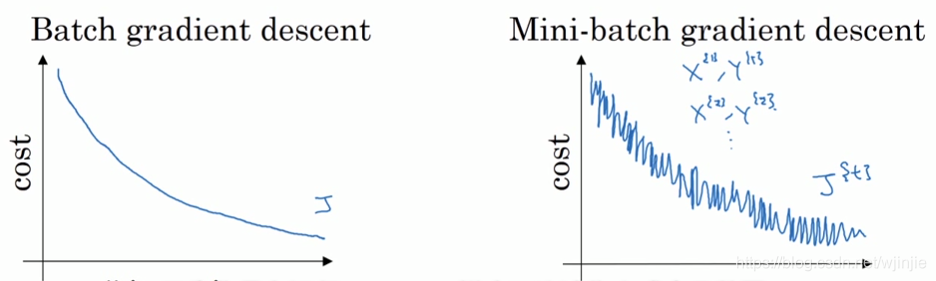
在这里插入图片描述
上图是BGD和MBGD训练时，损失代价函数的变化图。可见BGD能使代价函数逐渐减小，最终保证收敛到凸误差表面的全局最小值；MBGD的损失代价函数值比较振荡，但最终也能优化到损失最小值。

Momentum 主要引入了基于梯度的移动指数加权平均的思想，即当前的参数更新方向不仅与当前的梯度有关，也受历史的加权平均梯度影响。对于梯度指向相同方向的维度，动量会积累并增加，而对于梯度改变方向的维度，动量会减少更新。这也就使得收敛速度加快，同时又不至于摆动幅度太大。如下图红色线所示：
在这里插入图片描述

动量梯度下降（Momentum）的参数更新表达式如下所示：

在这里插入图片描述
其中， $\lambda$ 表示动量参数momentum；当 $\lambda=0$ 时，即是普通的SGD梯度下降。 $0<\lambda<1$ ，表示带了动量的SGD梯度下降参数更新方式， $\lambda$ 通常取0.9。

普通SGD的缺点：SGD很难在沟壑（即曲面在一个维度上比在另一个维度上弯曲得更陡的区域）中迭代，这在局部最优解中很常见。在这些场景中，SGD在沟壑的斜坡上振荡，同时沿着底部向局部最优方向缓慢前进。为了缓解这一问题，引入了动量momentum。

在这里插入图片描述

本质上，当使用动量时，如同我们将球推下山坡。球在滚下坡时积累动量，在途中变得越来越快。同样的事情发生在参数更新上：对于梯度指向相同方向的维度，动量会积累并增加，而对于梯度改变方向的维度，动量会减少更新。结果，我们获得了更快的收敛和减少的振荡。

RMSProp算法的全称叫 Root Mean Square Prop（均方根传递），是 Hinton 在 Coursera 课程中提出的一种优化算法，在上面的 Momentum 优化算法中，虽然初步解决了优化中摆动幅度大的问题。

为了进一步优化损失函数在更新中存在摆动幅度过大的问题，并且进一步加快函数的收敛速度，RMSProp算法对权重 W 和偏置 b 的梯度使用了微分平方加权平均数。优化后的效果如下：蓝色的为Momentum优化算法所走的路线，绿色的为RMSProp优化算法所走的路线。

在这里插入图片描述
假设在第 t 轮迭代过程中，各个公式如下所示：

在上面的公式中 $s_{dw}$ 和 $s_{db}$ 分别是损失函数在前 t?1轮迭代过程中累积的梯度平方动量， β 是梯度累积的一个指数。所不同的是，RMSProp 算法对梯度计算了微分平方加权平均数。这种做法有利于消除了摆动幅度大的方向，用来修正摆动幅度，使得各个维度的摆动幅度都较小。另一方面也使得网络函数收敛更快。

Adam 是另一种参数自适应学习率的方法，相当于 RMSprop + Momentum，利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。公式如下：

一阶矩和二阶矩 $m_t、v_t$ 类似于动量，将其初始化为： $m_{0}=0, v_{0}=0$

$m_t、v_t$ 分别是梯度的一阶矩（均值）和二阶矩（非中心方差）的估计值：

在这里插入图片描述
由于移动指数平均在迭代开始的初期会导致和开始的值有较大的差异，所以我们需要对上面求得的几个值做偏差修正。通过计算偏差校正的一阶和二阶矩估计来抵消这些偏差：

然后使用这些来更新参数，就像在 RMSprop 中看到的那样， Adam 的参数更新公式：
在这里插入图片描述

在Adam算法中，参数 β1 所对应的就是Momentum算法中的 β 值，一般取0.9，参数 β2 所对应的就是RMSProp算法中的 β 值，一般我们取0.999，而 ? 是一个平滑项，我们一般取值为 $10^{?8}$ ，而学习率则需要我们在训练的时候进行微调。

上一篇 : 求质数（素数）算法，及算法优化下一篇 : 抖音app官网版

奉行卓越设计
打造国际品质

傲世皇朝动态 NEWS真实、正向、传递价值