奉行卓越设计
打造国际品质

模型每次反向传导都会给各个可学习参数p计算出一个偏导数，用于更新对应的参数p。通常偏导数不会直接作用到对应的可学习参数p上，而是通过优化器做一下处理，得到一个新的值，处理过程用函数F表示（不同的优化器对应的F的内容不同），即，然后和学习率lr一起用于更新可学习参数p，即。

假设损失函数是，即我们的目标是学习x和y的值，让Loss尽可能小。如下是绘制损失函数的代码以及绘制出的结果。注意这并不是一个U型槽，它有最小值点，这个点对应的x和y值就是学习的目标。

通过解析求解，显然当时，Loss取得最小值。但这里我们通过神经网络反向传播求导的的方式，一步步优化参数，让Loss变小。通过这个过程，可以看出RMSProp算法的作用。

假设x和y的初值分别为，此时对Loss函数进行求导，x和y的梯度分别是，显然x将要移动的距离小于y将要移动的距离，但是实际上x离最优值0更远，差距是40，y离最优值0近一些，距离是20。因此SGD给出的结果并不理想。

RMSProp算法有效解决了这个问题。通过累计各个变量的梯度的平方r，然后用每个变量的梯度除以r，即可有效缓解变量间的梯度差异。如下伪代码是计算过程。

1. 初始：（这里只有两个可学习参数）
2. 初始：学习率?
3. 初始：平滑常数（或者叫做衰减速率）?
4. 初始：，加在分母上防止除0
5. 初始：梯度的平方?（有几个参数就有几个r）
6. while 没有停止训练 do
7. ? ? ? ? 计算梯度：
8. ? ? ? ? 累计梯度的平方：（也是一样的）
9. ? ? ? ? 更新可学习参数：（y的更新也是一样的）
10. end while

下图是训练10次，x和y的移动轨迹，其中红色对应SGD，蓝色对应RMSProp。观察SGD对应的红色轨迹，由于y的梯度很大，y方向移动过多，一下从坡一边跑到了另一边，而x的移动却十分缓慢。但是通过RMSProp，有效消除了梯度差异导致的抖动。

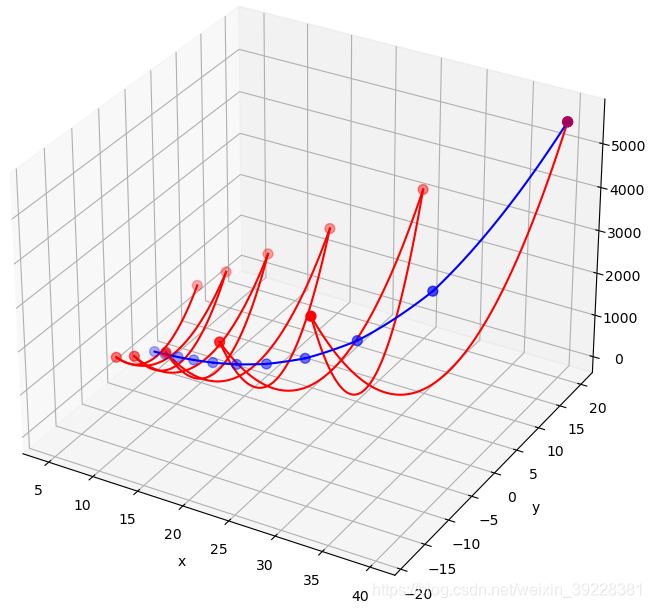
训练过程的代码如下。

接下来看下pytorch中的RMSProp优化器，函数原型如下，其中最后三个参数和RMSProp并无直接关系。

模型里需要被更新的可学习参数，即上文的x和y。

学习率。

平滑常数。

，加在分母上防止除0

weight_decay的作用是用当前可学习参数p的值修改偏导数，即：，这里待更新的可学习参数p的偏导数就是。

weight_decay的作用是正则化，和RMSProp并无直接关系。

根据上文伪代码第8行，计算出后，如果，则继续后面的计算，即。

否则计算过程变成，其中初始为0，是x的梯度，是上述累计的x的梯度的平方。

momentum和RMSProp并无直接关系。

如果centerd为False，则按照上述伪代码计算，即分母是。

否则计算过程变成，这里初始为0，然后分母依然是，但是不一样了。

centered和RMSProp并无直接关系，是为了让结果更平稳。