【Pytorch】第 8 章 ：实施政策梯度和政策优化
日期：2024-04-15 12:24:42 / 人气：
?🔎大家好，我是Sonhhxg_柒，希望你看完之后，能对你有所帮助，不足请指正！共同学习交流🔎
📝个人主页－Sonhhxg_柒的博客_CSDN博客?📃
🎁欢迎各位→点赞👍 + 收藏 + 留言📝?
📣系列专栏 - 机器学习【ML】?自然语言处理【NLP】? 深度学习【DL】
?🖍foreword
?说明?本人讲解主要包括Python、机器学习（ML）、深度学习（DL）、自然语言处理（NLP）等内容。
如果你对这个系列感兴趣的话，可以关注订阅哟👋
文章目录
在本章中，我们将重点介绍作为近年来最流行的强化学习技术之一的策略梯度方法。我们将从实施基本的 REINFORCE 算法开始，然后继续改进算法基线。我们还将实现更强大的算法、actor-critic 及其变体，并将其应用于解决 CartPole 和 Cliff Walking 问题。我们还将体验一个具有连续动作空间的环境，并求助于高斯分布来解决它。通过最后一个有趣的部分，我们将基于交叉熵方法训练一个代理来玩 CartPole 游戏。
本章将介绍以下食谱：
- 实施 REINFORCE 算法
- 使用基线开发 REINFORCE 算法
- 实施演员评论家算法
- 用 actor-critic 算法解决悬崖行走问题
- 设置连续的 Mountain Car 环境
- 利用演员-评论家网络解决连续的Mountain Car环境
- 通过交叉熵方法玩 CartPole
最近的一份出版物规定，政策梯度方法正变得越来越流行。他们的学习目标是优化动作的概率分布，使得给定一个状态，更有价值的动作将具有更高的概率值。在本章的第一个秘籍中，我们将讨论 REINFORCE 算法，它是高级策略梯度方法的基础。
REINFORCE算法也称为蒙特卡罗策略梯度，因为它基于蒙特卡罗方法优化策略。具体来说，它使用当前策略从一个事件中收集轨迹样本，并将它们用于策略参数 θ 。策略梯度的学习目标函数如下：
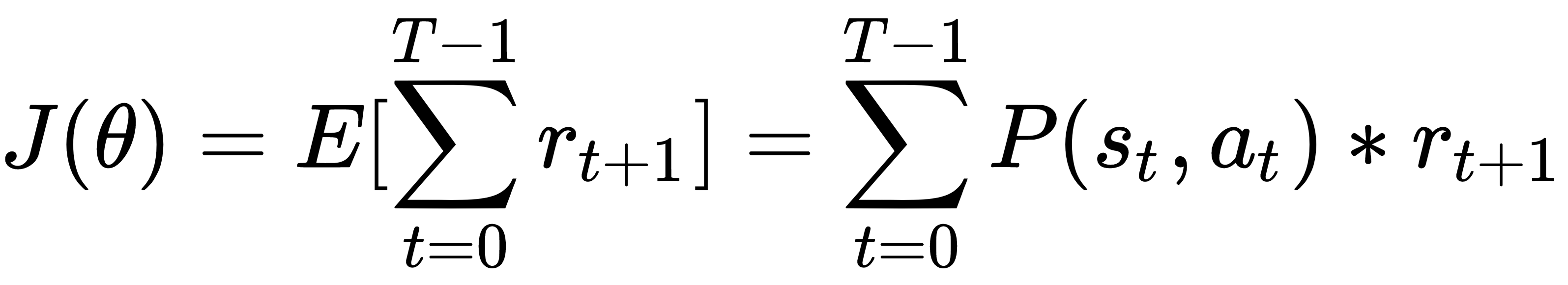
它的梯度可以推导如下：
在这里，
是回报，它是直到时间 t 的累积折扣奖励，并且是随机策略，它决定了在给定状态下采取某些行动的概率。由于策略更新是在整个剧集结束并收集所有样本后进行的，因此 REINFORCE 是一种 off-policy 算法。
在我们计算出策略梯度之后，我们使用反向传播来更新策略参数。使用更新后的策略，我们推出一集，收集一组样本，并使用它们重复更新策略参数。
我们现在将开发 REINFORCE 算法来解决 CartPole (?https://gym.openai.com/envs/CartPole-v0/?) 环境。
我们开发了 REINFORCE 算法来解决 CartPole 环境，如下所示：
1.导入所有必要的包并创建一个 CartPole 实例：
2.让我们从类的开始__init__method，PolicyNetwork?它使用神经网络来近似策略：
3.接下来，添加predict计算估计策略的方法：
4.我们现在开发训练方法，它使用在一集中收集的样本更新神经网络：
5.该类的最终方法PolicyNetwork是get_action，它根据预测的策略对给定状态的动作进行采样：
它还返回所选动作的对数概率，这将用作训练样本的一部分。
这就是课堂的全部内容PolicyNetwork！
6.现在，我们可以继续使用策略网络模型开发REINFORCE算法：
7.我们指定策略网络的大小（输入层、隐藏层和输出层）、学习率，然后PolicyNetwork相应地创建一个实例：
我们将折扣因子设置为0.9：
8.我们使用刚刚为 500 集开发的策略网络使用 REINFORCE 算法进行学习，我们还跟踪每一集的总奖励：
9.现在让我们展示情节奖励随时间变化的情节：
在步骤 2中，为简单起见，我们使用具有一个隐藏层的神经网络。策略网络的输入是一个状态，后面跟着一个隐藏层，而输出是采取可能的单个动作的概率。因此，我们使用 softmax 函数作为输出层的激活。
第 4 步是更新网络参数：给定一个 episode 中收集的所有数据，包括所有步骤的返回和对数概率，我们计算策略梯度，然后通过反向传播相应地更新策略参数。
在第 6 步中，REINFORCE 算法执行以下任务：
- 它运行一个 episode：对于 episode 中的每个步骤，它根据当前估计的策略对一个动作进行采样；它存储每一步的奖励和日志策略。
- 一旦一个情节结束，它就会计算每一步的折扣累积奖励；它通过减去它们的平均值然后除以它们的标准差来标准化结果回报。
- 它使用返回和对数概率计算策略梯度，然后更新策略参数。我们还显示每一集的总奖励。
- 它n_episode通过重复上述步骤来运行剧集。
第 8 步将生成以下训练日志：
您将在第 9 步中观察到以下图：
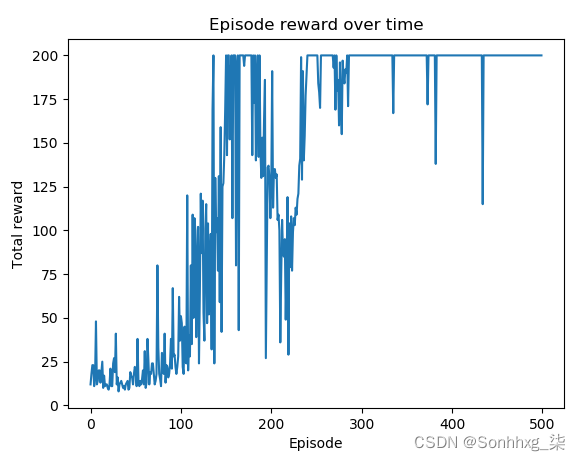
可以看到最近200集的大部分都有最高+200的奖励。
REINFORCE 算法是一族策略梯度方法，通过以下规则直接更新策略参数：
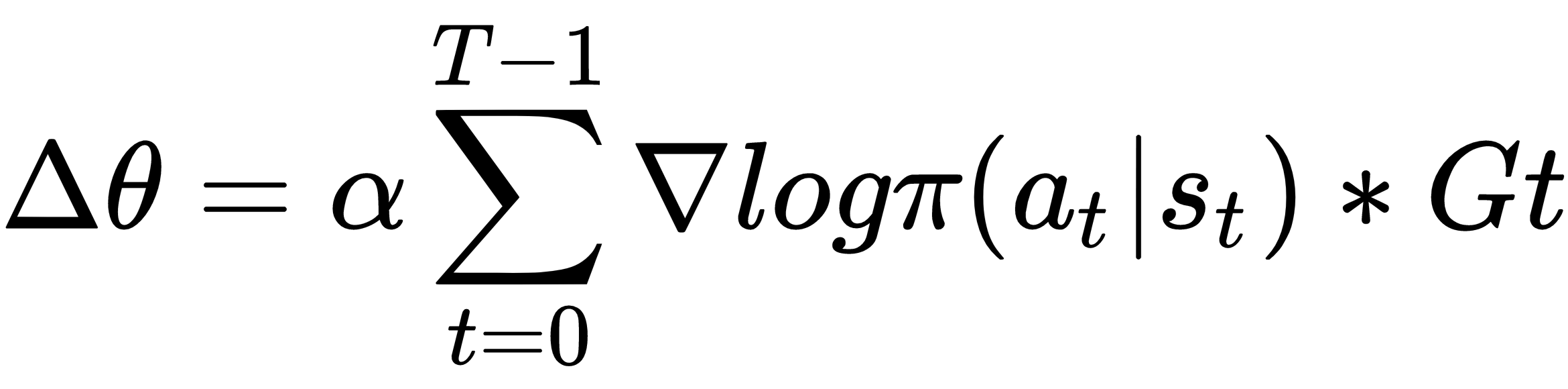
这里，α 是学习率，
作为动作的概率映射，作为累积折扣奖励，是在一个情节中收集的经验。由于训练样本集是在完整情节完成后才构建的，因此 REINFORCE 中的学习是以一种离策略的方式进行的。学习过程可以总结如下：
- 随机初始化策略参数θ。
- 通过根据当前策略选择操作来执行一集。
- 在每一步，存储所选动作的对数概率以及产生的奖励。
- 计算各个步骤的回报。
- 使用对数概率和回报计算策略梯度，并通过反向传播更新策略参数 θ。
- 重复步骤 2至5。
同样，由于 REINFORCE 算法依赖于随机策略生成的完整轨迹，因此它构成了蒙特卡罗方法。
推导策略梯度方程非常棘手。它利用对数导数技巧。如果您想知道，这里有一个详细的解释：
在 REINFORCE 算法中，蒙特卡罗在用于更新策略的情节中播放整个轨迹。然而，随机策略可能会在不同的 episode 中对相同的状态采取不同的动作。这可能会混淆训练，因为一个采样体验想要增加选择一个动作的概率，而另一个采样体验可能想要降低它。为了减少 vanilla REINFORCE 中的这种高方差问题，我们将在这个秘籍中开发一种变异算法，REINFORCE with baseline。
在 REINFORCE with baseline 中，我们从返回 G 中减去基线状态值。因此，我们在梯度更新中使用优势函数 A，其描述如下：
这里，V(s) 是估计给定状态的状态值的值函数。通常，我们可以使用线性函数或神经网络来近似状态值。通过引入基线值，我们可以根据给定状态的平均动作来校准奖励。
我们使用两个神经网络（一个用于策略，另一个用于价值估计）开发具有基线算法的 REINFORCE，以解决 CartPole 环境。
我们使用 REINFORCE with baseline 算法解决 CartPole 环境，如下所示：
1.导入所有必要的包并创建一个 CartPole 实例：
2.PolicyNetwork对于策略网络部分，它与我们在实现 REINFORCE 算法一节中使用的类基本相同。请记住，update?方法中使用了优势值：
3.对于价值网络部分，我们使用带有一个隐藏层的回归神经网络：
它的学习目标是近似状态值；因此，我们使用均方误差作为损失函数。
该update?方法当然通过反向传播使用一组输入状态和目标输出来训练价值回归模型：
该predict?方法估计状态值：
4.现在，我们可以继续使用具有策略和价值网络模型的基线算法开发 REINFORCE：
5.我们指定策略网络的大小（输入层、隐藏层和输出层）、学习率，然后PolicyNetwork相应地创建一个实例：
至于价值网络，我们也设置它的大小并创建一个实例：
我们将折扣因子设置为0.9：
6.我们使用 REINFORCE 和基线算法对 2,000 集进行学习，我们还跟踪每集的总奖励：
7.现在，我们显示情节奖励随时间变化的情节：
REINFORCE 在很大程度上依赖于蒙特卡罗方法来生成用于训练策略网络的整个轨迹。然而，在相同的随机策略下，不同的事件可能会采取不同的行动。为了减少采样体验的方差，我们从返回中减去状态值。由此产生的优势衡量相对于平均动作的奖励，这将用于梯度更新。
在第 4 步中，使用基线算法的 REINFORCE 执行以下任务：
- 它运行一个 episode——每一步的状态、奖励和日志策略。
- 一旦一个情节结束，它就会计算每一步的折扣累积奖励；它使用价值网络估计基线值；它通过从收益中减去基线值来计算优势值。
- 它使用优势值和对数概率计算策略梯度，并更新策略和价值网络。我们还显示每一集的总奖励。
- 它n_episode通过重复上述步骤来运行剧集。
执行第 7 步中的代码将产生以下图：
可以看到在 1200 集左右后性能非常稳定。
使用附加值基线，我们能够重新校准奖励并减少梯度估计的方差。
在 REINFORCE with baseline 算法中，有两个独立的组件，策略模型和价值函数。我们实际上可以将这两个组件的学习结合起来，因为学习价值函数的目标是更新策略网络。这就是actor-critic算法所做的，我们将在这个秘籍中开发它。
actor-critic 算法的网络由以下两部分组成：
- Actor：接受输入状态并输出动作概率。本质上，它通过使用评论家提供的信息更新模型来学习最优策略。
- Critic：这通过计算价值函数来评估输入状态的好坏。该值指导参与者如何调整。
这两个组件共享网络中输入层和隐藏层的参数，因为以这种方式学习比单独学习它们更有效。因此，损失函数是两部分的总和，具体来说，衡量演员的行为的负对数似然，以及衡量评论家的估计和计算回报之间的均方误差。
一个更流行的 actor-critic 算法版本是Advantage Actor-Critic?(?A2C?)。顾名思义，critic 部分计算的是优势值，而不是状态值，这类似于 REINFORCE with baseline。它评估一个动作在某种状态下与其他动作相比有多好，并且已知可以减少策略网络中的方差。
我们开发了 actor-critic 算法来解决 CartPole 环境，如下所示：
1.导入所有必要的包并创建一个 CartPole 实例：
2.让我们从 actor-critic 神经网络模型开始：
3.我们继续使用 actor-critic 神经网络__init__的类方法：PolicyNetwork
4.接下来，我们添加predict计算估计动作概率和状态值的方法：
5.我们现在开发该training方法，该方法使用在一集中收集的样本更新神经网络：
6.该类的最后一个方法PolicyNetwork是 get_action，它根据预测的策略对给定状态的动作进行采样：
它还返回所选动作的对数概率，以及估计的状态值。
这就是PolicyNetwork?课堂的全部内容！
7.现在，我们可以继续开发 main 函数，训练一个 actor-critic 模型：
8.我们指定策略网络的大小（输入层、隐藏层和输出层）、学习率，然后PolicyNetwork相应地创建一个实例：
我们将折扣因子设置为0.9：
9.我们使用刚刚为 1,000 集开发的策略网络通过演员-评论家算法进行学习，我们还跟踪每集的总奖励：
10.最后，我们展示 episode reward 随时间变化的情节：
正如您在步骤 2中看到的，演员和评论家共享输入层和隐藏层的参数；actor 的输出由采取单个动作的概率组成，critic 的输出是输入状态的估计值。
在第 5 步中，我们计算优势值及其负对数似然。actor-critic 中的损失函数是优势的负对数似然与返回值和估计状态值之间的均方误差的组合。smooth_l1_loss请注意，如果绝对误差低于 1，我们使用，这是一个平方项，否则使用绝对误差。
在步骤 7中，actor-critic 模型的训练函数执行以下任务：
- 它运行一个 episode：对于 episode 中的每个步骤，它根据当前估计的策略对一个动作进行采样；它存储每一步的奖励、日志策略和估计的状态值。
- 一旦一个情节结束，它就会计算每一步的折扣累积奖励；它通过减去它们的平均值然后除以它们的标准差来标准化结果回报。
- 它使用返回值、对数概率和状态值来更新策略参数。我们还显示每一集的总奖励。
- 如果一集的总奖励超过 +195，我们会稍微降低学习率。
- 它n_episode通过重复上述步骤来运行剧集。
执行第 9 步中的训练后，您将看到以下日志：
下图是第 10 步的结果：
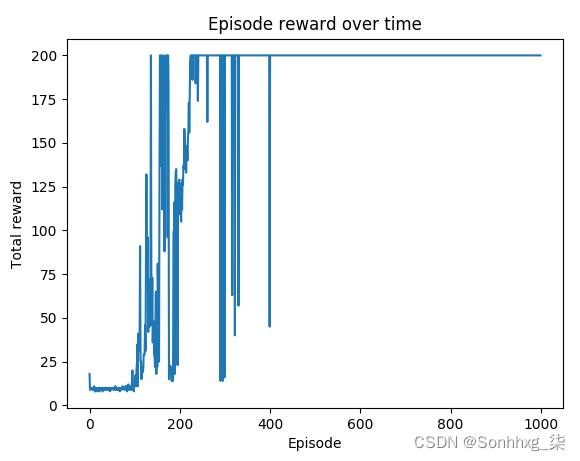
可以看到400集左右后的奖励保持在最大值+200。
在 advantage actor-critic 算法中，我们将学习分解为两部分——actor 和 critic。A2C 中的 Critic 评估一个动作在一个状态下的好坏，它指导演员应该如何反应。同样，优势值计算为 A(s,a) = Q(s,a) -V(s)，这意味着从 Q 值中减去状态值。Actor 根据 critic 的指导估计动作概率。优势的引入可以减少方差，因此，A2C 被认为是比标准演员评论家更稳定的模型。正如我们在 CartPole 环境中看到的那样，A2C 在经过数百个 episode 的训练后，性能一直保持一致。它在基线方面优于 REINFORCE。
在这个秘籍中，让我们使用 A2C 算法解决一个更复杂的悬崖行走环境。
Cliff Walking 是一种典型的 Gym 环境，具有长剧集且无法保证终止。这是一个4 * 12板的网格问题。智能体在一个步骤中进行上、右、下和左移动。左下角的图块是代理的起点，右下角的图块是获胜点，如果到达该点，情节将结束。最后一行剩下的方块是悬崖，代理人踩到其中任何一个后都会重置到起始位置，但情节仍在继续。智能体采取的每一步都会产生 -1 奖励，但踩到悬崖除外，在悬崖上会产生 -100 奖励。
state是一个0到47的整数，表示agent所在的位置，如图：
?该值不包含数字含义。例如，处于状态 30 并不意味着它与处于状态 10 的状态有 3 倍的不同。因此，在将状态提供给策略网络之前，我们将首先将其转换为单热编码向量。
我们使用 A2C 算法解决 Cliff Walking 问题，如下所示：
1.导入所有必要的包并创建一个 CartPole 实例：
2.随着状态变为 48 维，我们使用了一个更复杂的具有两个隐藏层的 actor-critic 神经网络：
同样，演员和评论家共享输入层和隐藏层的参数。
3.我们继续使用刚刚在步骤 2PolicyNetwork中开发的演员-评论家神经网络上课。它与实现 actor-critic 算法一节中的类相同。PolicyNetwork
4.接下来，我们开发 main 函数，训练一个 actor-critic 模型。它与实施 actor-critic 算法一节中的几乎相同，只是将状态额外转换为 one-hot 编码向量：
5.我们指定策略网络的大小（输入层、隐藏层和输出层）、学习率，然后PolicyNetwork相应地创建一个实例：
我们将折扣因子设置为0.9：
6.我们使用刚刚为 1,000 集开发的策略网络通过演员-评论家算法进行学习，我们还跟踪每集的总奖励：
7.现在，我们展示从第 100 集开始的每集奖励随时间变化的图：
您可能会注意到，在第 4 步中，如果某集的总奖励超过 -14，我们会略微降低学习率。-13 的奖励是我们能够通过路径 36-24-25-26-27-28-29-30-31-32-33-34-35-47 实现的最大值。
执行第 6 步中的训练后，您将看到以下日志：
下图是第 7 步的结果：
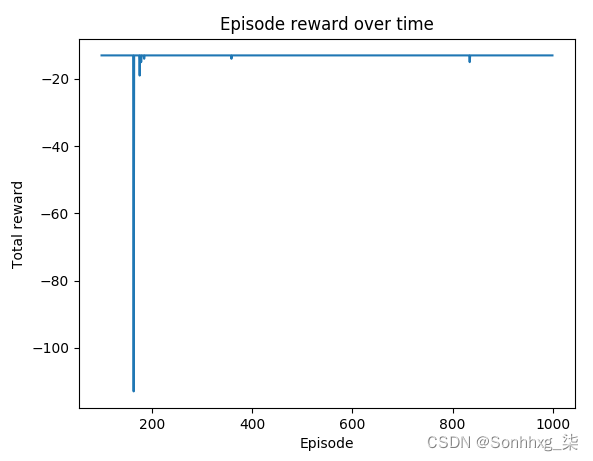
?正如我们所观察到的，在第 180 集左右之后，大多数集中的奖励都达到了最优值 -13。
在这个秘籍中，我们用 A2C 算法解决了悬崖行走问题。由于从 0 到 47 的整数状态表示代理在 4*12 棋盘中的位置，不包含数字含义，因此我们首先将其转换为 48 维的单热编码向量。为了处理 48 维的输入，我们使用了一个稍微复杂的具有两个隐藏层的神经网络。A2C 在我们的实验中被证明是一种稳定的策略方法。
到目前为止，我们所处理的环境具有离散的动作值，例如 0 或 1，代表向上或向下、向左或向右。在这个秘籍中，我们将体验具有连续动作的山地车环境。
Continuous Mountain Car（MountainCarContinuous v0 · openai/gym Wiki · GitHub）是一个具有连续动作的Mountain Car环境，其值是从-1到1。如下截图所示，它的目标是把车开到右手边的山顶：
在一维赛道中，汽车位于 -1.2（最左边）和 0.6（最右边）之间，目标（黄旗）位于 0.5。汽车的发动机不够强劲，无法一次将其推上山顶，因此它必须来回行驶以积蓄动力。因此，动作是一个浮点数，表示如果它是从 -1 到 0 的负值，则表示将汽车向左推的力，如果它是从 0 到 1 的正值，则表示将汽车向右推的力。
环境有两种状态：
- 汽车的位置：这是一个从 -1.2 到 0.6 的连续变量
- 汽车的速度：这是一个从 -0.07 到 0.07 的连续变量
起始状态由 -0.6 到 -0.4 之间的位置和 0 的速度组成。
与每个步骤相关的奖励是-a?2，其中 a 是动作。并且达成目标还有+100的额外奖励。因此，它会惩罚在汽车到达目标之前每一步所用的力。当汽车到达目标位置（显然）或 1,000 步后，一集结束。
让我们通过观察以下步骤来模拟连续的 Mountain Car 环境：
1.我们导入 Gym 库并创建连续 Mountain Car 环境的实例：
2.看一下动作空间：
3.然后我们重置环境：
汽车以状态 [-0.56756635, 0. ] 开始，这意味着初始位置在 -0.56 左右，速度为 0。您可能会看到不同的初始位置，因为它是从 -0.6 到 -0.4 随机生成的。
4.现在让我们采用一种简单的方法：我们只是采取从 -1 到 1 的随机操作：
状态（位置和速度）不断变化，每一步的奖励是-a?2 。
您还会在视频中看到汽车反复向右和向左移动。
可以想象，连续的 Mountain Car 问题是一个具有挑战性的环境，甚至比只有三种不同可能动作的原始离散问题更具挑战性。我们需要来回驾驶汽车，以适当的力量和方向建立动力。此外，动作空间是连续的，这意味着值查找/更新方法（如TD方法、DQN）将不起作用。在下一个秘籍中，我们将使用 A2C 算法的连续控制版本来解决连续山地车问题。
在这个秘籍中，我们将使用优势 actor-critic 算法解决连续的 Mountain Car 问题，当然这次是连续版本。您将看到它与离散版本有何不同。
正如我们在 A2C 中看到的具有离散动作的环境一样，我们根据估计的概率对动作进行采样。既然我们不能对无数的连续动作进行这样的采样，我们如何模拟一个连续的控制？我们实际上可以求助于高斯分布。我们可以假设动作值服从高斯分布：
此处，均值
和偏差
是从策略网络计算得出的。通过这个调整，我们可以通过当前均值和偏差从构建的高斯分布中采样动作。连续A2C中的损失函数类似于我们在离散控制中使用的损失函数，它是用高斯分布下的动作概率和优势值计算的负对数似然，以及实际返回值和估计值之间的回归误差的组合状态值。
?请注意，一个高斯分布用于模拟一维的动作，因此，如果动作空间为 k 维，则需要使用 k 个高斯分布。在连续的 Mountain Car 环境中，动作空间是一维的。A2C 在连续控制方面的主要困难是如何构建策略网络，因为它计算高斯分布的参数。
我们使用连续 A2C 解决连续 Mountain Car 问题，如下所示：
1.导入所有必要的包并创建一个连续的 Mountain Car 实例：
2.让我们从 actor-critic 神经网络模型开始：
3.我们继续使用我们刚刚开发的 actor-critic 神经网络__init__的类方法：PolicyNetwork
4.接下来，我们添加predict计算估计动作概率和状态值的方法：
5.我们现在开发训练方法，该方法使用在一集中收集的样本更新策略网络。我们将重用在实施 actor-critic 算法一节中开发的更新方法，此处不再重复。
6.该类的最终方法PolicyNetwork是get_action，它从给定状态的估计高斯分布中采样一个动作：
它还返回所选动作的对数概率和估计的状态值。
这就是连续控制类的全部内容PolicyNetwork?！
现在，我们可以继续开发 main 函数，训练一个 actor-critic 模型：
7.该scale_state函数用于规范化（标准化）输入以加快模型收敛速度。我们首先随机生成 10,000 个观察值并使用它们来训练缩放器：
一旦缩放器被训练，我们就在scale_state函数中使用它来转换新的输入数据：
8.我们指定策略网络的大小（输入层、隐藏层和输出层）、学习率，然后PolicyNetwork相应地创建一个实例：
我们将折扣因子设置为0.9：
9.我们使用我们刚刚开发的策略网络对 200 集执行连续控制，我们还跟踪每集的总奖励：
10.现在，让我们展示情节奖励随时间变化的情节：
在这个秘籍中，我们使用高斯 A2C 来解决连续的 Mountain Car 环境。
在步骤 2中，我们示例中的网络有一个隐藏层。输出层中有三个独立的组件。它们是高斯分布的均值和偏差，以及状态值。使用 tanh 激活函数将分布均值的输出缩放到 [-1, 1]（或本例中的 [-2, 2]）的范围。至于分布偏差，我们使用softplus作为激活函数来保证正偏差。网络返回当前的高斯分布（参与者）和估计的状态值（评论家）。
第 7 步中 actor-critic 模型的训练函数与我们在实施 actor-critic 算法一节中开发的非常相似。您可能会注意到，我们为采样动作添加了一个值剪辑，以使其保持在 [-1, 1] 范围内。scale_state?我们将在接下来的步骤中解释该函数的作用。
执行第 10 步中的训练后，您将看到以下日志：
下图是第 11 步的结果：
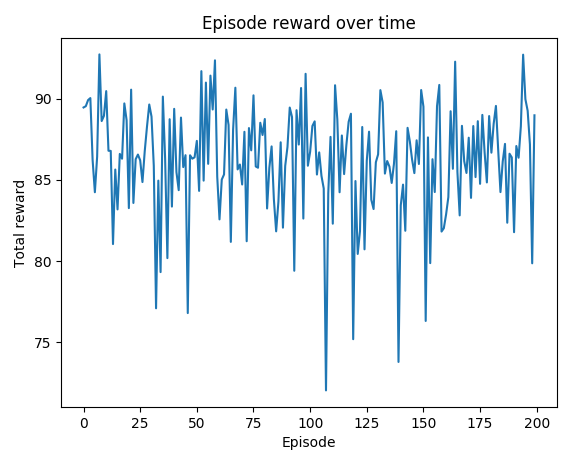
根据MountainCarContinuous v0 · openai/gym Wiki · GitHub中的解决要求，获得+90 以上的奖励即为解决环境。我们有多集解决环境问题。
在连续 A2C 中，我们假设动作空间的每个维度都是高斯分布的。高斯分布的均值和偏差是策略网络输出层的一部分。输出层的其余部分用于估计状态值。一个动作（或一组动作）是从由当前均值和偏差参数化的高斯分布中采样的。连续 A2C 中的损失函数与其离散版本类似，它是结合高斯分布下的动作概率和优势值计算的负对数似然，以及实际返回值和估计状态值之间的回归误差。
到目前为止，我们一直以随机方式对策略建模，我们从分布或计算的概率中对动作进行采样。作为奖励部分，我们将简要讨论确定性策略梯度(?DPG?)，我们将策略建模为确定性决策。我们通过将输入状态直接映射到动作而不是动作概率，简单地将确定性策略视为随机策略的特例。DPG算法一般使用以下两组神经网络：
- Actor-critic network：这和我们体验过的A2C很像，但是是确定性的方式。它预测状态值和要采取的行动。
- Target actor-critic network：这是演员-评论家网络的定期副本，目的是稳定学习。显然，您不希望目标不断变化。该网络为训练提供了时间延迟的目标。
如您所见，DPG 中并没有太多新内容，而是 A2C 和延时目标机制的完美结合。随意自己实现算法并用它来解决连续的 Mountain Car 环境。
如果您对 softplus 激活不熟悉，或者想了解更多有关 DPG 的信息，请查看以下资料：
- Softplus： https:?//en.wikipedia.org/wiki/Rectifier_(neural_networks)
- DFP原论文：https://hal.inria.fr/file/index/docid/938992/filename/dpg-icml2014.pdf
在最后一个秘籍中，通过奖励（和有趣的）部分，我们将开发一个简单但功能强大的算法来解决 CartPole。它基于交叉熵，将输入状态直接映射到输出动作。事实上，它比本章中的所有其他策略梯度算法更直接。
我们应用了几种策略梯度算法来解决 CartPole 环境。他们使用复杂的神经网络架构和损失函数，这对于像 CartPole 这样的简单环境来说可能有点矫枉过正。为什么我们不直接预测给定状态的动作？这背后的想法很简单：我们对从状态到动作的映射进行建模，并仅使用过去最成功的经验对其进行训练。我们只对正确的行为应该是什么感兴趣。在这种情况下，目标函数是实际和预测动作之间的交叉熵。在 CartPole 中，有两种可能的动作：向左和向右。为了简单起见，我们可以用下面的模型图将其转化为二分类问题：
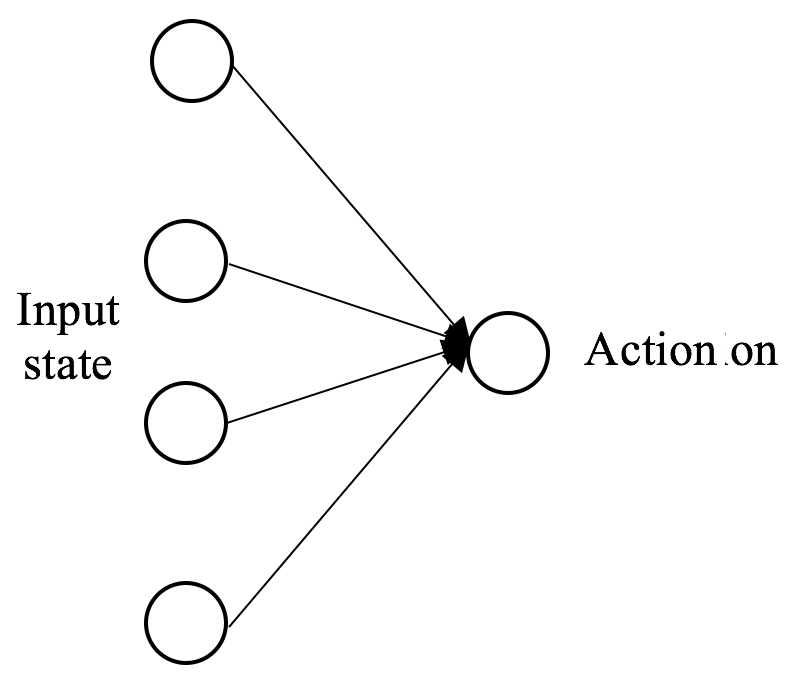
我们使用交叉熵解决 CartPole 问题，如下所示：
1.导入所有必要的包并创建一个 CartPole 实例：
2.让我们从动作估计器开始：
3.我们现在开发交叉熵算法的主要训练函数：
4.然后我们指定动作估计器的输入大小和学习率：
然后我们Estimator?相应地创建一个实例：
5.我们将生成 5,000 个随机片段并挑选出最好的 10,000 个（状态、动作）对来训练估计器：
6.模型训练好后，我们来测试一下。我们用它来播放 100 集并记录总奖励：
7.然后我们将性能可视化如下：
正如您在步骤 2中看到的，动作估计器有两层——输入层和输出层，后面是一个 sigmoid 激活函数，损失函数是二元交叉熵。
第三步是训练交叉熵模型。具体来说，对于每个训练情节，我们采取随机行动，累积奖励，并记录状态和行动。在经历过n_episode?episode 之后，我们将最成功的 episode（总奖励最高）和n_samples?（状态，动作）对的提取作为训练样本。然后，我们在刚刚构建的训练集上训练估计器进行 100 次迭代。
执行第 7 步中的代码行将产生以下图：
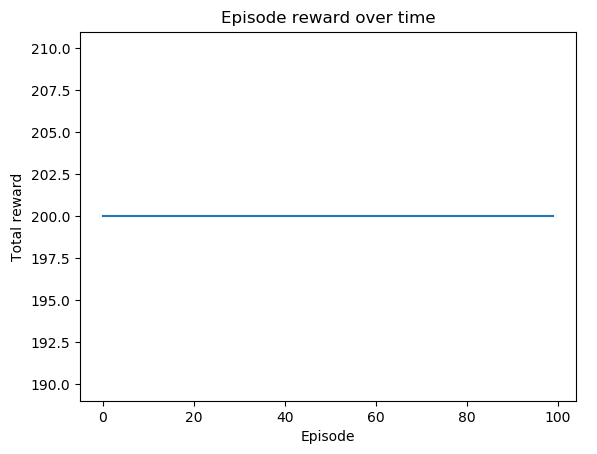
如您所见，所有测试剧集都有+200的奖励！
对于简单的环境，交叉熵非常简单但很有用。它直接模拟输入状态和输出动作之间的关系。控制问题被构建为分类问题，我们试图在所有备选方案中预测正确的行动。诀窍在于我们只从正确的经验中学习，这些经验指导模型在给定状态下最有价值的行动应该是什么。
