奉行卓越设计
打造国际品质

差分进化算法(Differential Evolution ，DE)是一种新兴的进化计算技术。它起源于解决切比雪夫多项式问题，现在DE广泛用于解决复杂优化问题，并且取得非常不错的效果。差分进化算法是一种基于差分信息进行自适应寻优的全局优化算法，主要包括变异、杂交和选择三个算子，属于智能算法的一种，其易于实现、鲁棒性强、控制参数少，因此被广泛的应用在各个领域。差分进化是模拟自然界生物随机进化的一种模型，通过反复的迭代进化，保留那些更适应环境的个体，类似于自然界的物竞天择，适者生存。相比其它的进化算法，差分进化算法采用实数编码、基于差分的变异操作和一对一的竞争选择策略，使得遗传操作简单易实现。差分进化算法因其特有的全局记忆能力，可以动态的检测当前的进化状态来调整其搜索策略，具有较强的搜索能力，并且对问题的特征信息不敏感，可以应用在各种复杂环境下，非常适合于求解多极值、高维度的复杂数学优化问题。与此同时，差分进化算法也存在收敛速度慢、容易陷入局部最优的问题。

变异是差分进化算法最显著的特点，个体间的差分信息驱动DE算法的进化方向。种群中的个体按照一定的顺序执行来执行变异，根据选择的变异策略来挑选相应的个体，执行变异操作生成新的临时个体。基本差分变异策略有以下五种：

(1) DE/rand/1:

(2) DE/best/1:

(3) DE/current-to-best/1：

(4) DE/rand/2：

(5) DE/best/2：

其中 为当前种群中不同的随机个体下标，i表示当前个体下标，best表示当前全局最优个体下标，F为控制参数缩放因子。

以DE/current-to-best/1变异算子为例，差分进化算法在二维空间的变异算子示意图如下所示：

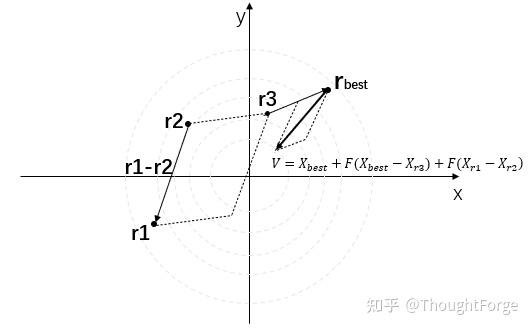
根据一定的概率从多个个体中挑选基因，重新组合成一个新的个体，实现基因重组就是交叉操作，此概率就是交叉因子CR。通过变异操作产生的一个临时变异向量 ，然后与当前个体进行交叉，得到一个新的个体 ，交叉式子如下所示：

其中rand是0到1之间随机数，通常满足均匀分布，jrand是随机生成的介于1~D之间的整数，D是向量最大维度，示意图如下：

经过交叉操作(基因重组)后得到的新的个体U，计算出适应度值，并与当前个体X的适应度值进行比较，如果新个体U的适应度值较好，那么此次迭代认为是一次成功迭代，新个体U将会保留到下一代，当前个体X被淘汰，反之则是一次无用迭代，只保留当前个体X，选择策略公式如下：

式子中，为个体 的适应度值， 为个体的适应度值，在本章中的实验部分，测试函数计算所得的适应度值小的认为是较优秀的，具体的优劣性根据实际情况而定。

DE算法的流程示意图如下图2.3所示：

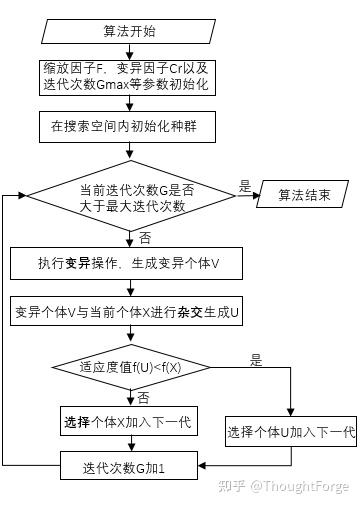
基本差分进化算法的算法步骤如下所示：

BEGIN

Step1：参数初始化。初始化超参数交叉概率Cr、缩放比例F以及最大进化次数G，并设置当前进化次数g=1；

Step2：初始化种群。根据种群个体数量NP以及问题维度D，在搜索空间内随机初始化种群；

Step3：算法结束判断。根据当前进化次数g是否大于G，若是则终止循环，否则继续；

Step4：一次算法迭代。对于种群中的每个个体Xi执行下列操作：

St4.1：在种群中随机选取三个不同的个体r1、r2、r3，且

St4.2：随机产生一个范围在[1,D]的整数Z；

St4.3：对于个体Xi的每一维j执行如下操作：

St4.3.1：随机生成一个在[0,1]上均匀分布的数r；

St4.3.2：若r<=CR或者j==Z，则执行DE/rand/1，否则不变；

St4.4：通过目标函数的适应度值来评估当前个体和实验个体实行优胜劣汰；

Step5：g=g+1，返回Step3。

END